离心通风机刚度计算方法-博天堂在线开户

1  概述

离心通风机叶轮由于刚度差而导致失效的现象时有发生。其机理为叶片受离心力作用而弯曲变形，且各叶片弯曲变形的程度又不可能完全相同，因而使平衡遭到破坏，以致于最后失效。尤其是宽径比比较大的风机，如4－73、4－60、6－40等，在高圆周速度条件下，这个问题就更为突出。此外，在实际工作中，还会经常遇到为解决耐磨问题而将4－73的机翼型叶片改为板式叶片的情况，显然，其刚度会明显下降。为此，通常采用增加副前盘的结构方案进行解决，如图1所示；但在何种条件下加副前盘以及设计成何种形式的副前盘，则依靠设计者的经验。然而，是否成功则需要在试验台或工业现场进行考核。

因此，在设计阶段对离心通风机叶轮的刚度进行计算是很有必要的，也是必须得完成的一个项目。但目前笔者能查阅到的只是在文献[1]中提到的刚度校核公式，而实际应用时，却发现还有一些问题无法解决：一是该公式没有推导过程。因而，对其建模过程不了解；二是具体变形量无具体数值。因而，对不同的风机或不同的使用场合，如何提出变形控制指标就无从下手；三是按此公式计算刚度，如果结果达不到要求，设计成何种形式的副前盘也无法判断，因为不知道叶片上何处刚性薄弱。

因此，确定适用的离心通风机刚度的工程计算方法，对风机的设计、工艺和生产有重要作用。

2  计算模型的建立

离心通风机叶轮由前盘、叶片、后盘或中盘，焊接或铆接而成。多数叶轮的前盘均有锻件或铆焊件进口圈，而且部分叶轮的前盘在靠近外缘部位还焊接有多种形式的调频环以加强其刚性；而后盘或中盘一般厚度较大（不少叶轮后盘或中盘还有锻件辐板或焊接辐板），用螺栓与铸件轮毂或主轴联接。因此，就风机叶轮结构和工作特点而言，前盘和后盘或中盘的刚性较强，而叶片的刚性相对较弱，叶轮刚性问题也就表现为叶片的刚性问题。所以，在设计和生产中，保证了叶片的刚度也就保证了整个离心叶轮的刚度。

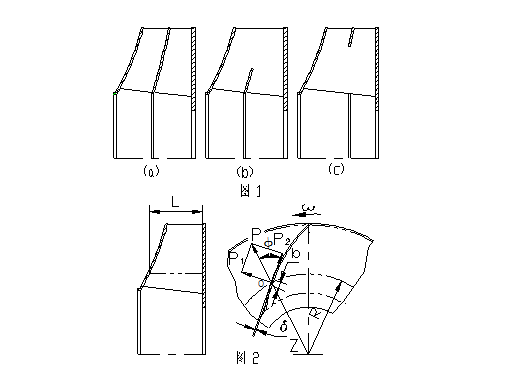
对叶片的受力情况进行初步分析：与叶片自身离心力相比，其受到的气动力的数量级太小，在计算刚度时可忽略不计。因此，应主要考虑叶片离心力的影响。沿着叶片型线从进口到出口边，由于半径和方向的变化，其离心力的大小和方向也在变化，不可否认，其变形量的大小也会随着半径的不同而变化，即其变形不是均匀的；但沿着叶轮轴向方向，可以认为其沿叶片宽度方向受均布载荷。也就是说，可以把叶片看成沿叶片宽度方向受均布载荷的固定梁（如焊接叶轮）或简支梁（如铆接叶轮），这是建立数学模型的基础。

3  计算公式的推导

3.1  钢制板式后弯叶片焊接叶轮

为了分析不同半径处叶片的变形量，如图2所示，可取任意一个叶片，假设在半径r处取一微元b ，其厚度为δ，其长度（即叶片宽度）为l，则该微元在旋转角速度ω(1/rad)或转速n下产生离心力p, 该p值又可分解成p₁和p₂。沿p₂方向叶片抗弯模量极大，可以忽略p₂产生的变形。因此，计算和控制p₁产生的变形则是主要矛盾。作为均布载荷，若p₁=q l，则该微元就可简化成如图3所示的受均布载荷的固定梁模型。

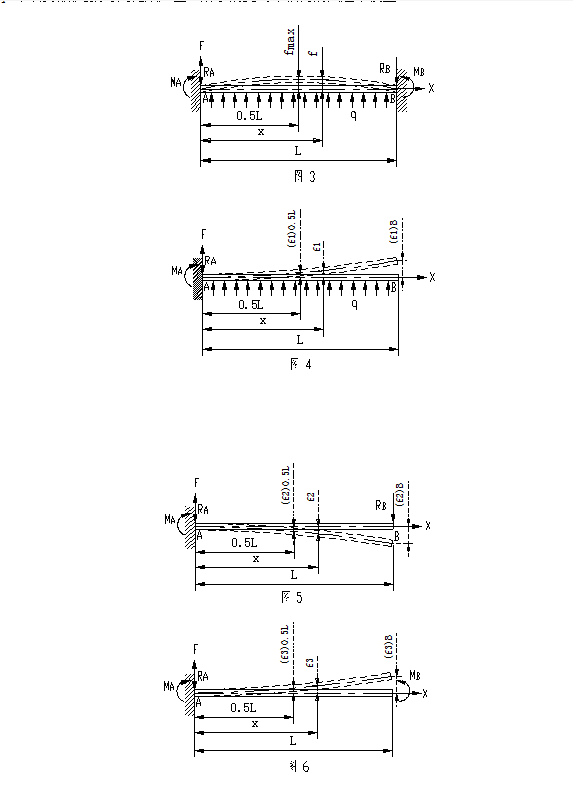
在材质具有连续性、均匀性、各向同性和变形控制在弹性变形范围内的假设下，上述计算模型就把叶轮的刚度问题转化成求解该微元的最大变形并控制该变形量的问题。

设材质的弹性模量为e，微元的惯性矩为i。分析图3，显然，m_a=m_b，r_a=r_b=0.5ql，其最大变形发生在0.5l处；并且边界约束条件为在x=0或x=l时，f=0。由于其为静不定结构，需要另外寻求变形协调方程。应用线性叠加原理，则图3的模型可以分解成图4、图5和图6三个模型，也就是前者是后三者的线形叠加，于是：

 f  =  f₁  f₂   f₃                                               (1 )

 (f )_b =  (f₁) _b  (f₂) _b  (f₃) _b                                       (1a )

f_max =  (f₁) _0.5l  (f₂) _0.5l  (f₃) _0.5l                                                  (1b )

• 受均布载荷q的悬臂梁（见图4）

其变形曲线方程为

f₁ = q x²  *  ( x² － 4 l x  6 l²   ）/ （ 24 e i ）                       （2 )

在b点，其变形量为

                           （f₁）_b =      q l⁴   / （8 e i ）                               (2a )

在0.5l点，其变形量为

                 （f₁）_0.5l =     17q l⁴  / （384 e i ）                              (2b )

   (2) 受集中载荷r_b的悬臂梁（见图5）

其变形曲线方程为

f₂ = －  q x²   ( 3l  － x  ) l  /  （12 e i ）                        (3 )

 在b点，其变形量为

（f₁）_b = -q l⁴  /  （ 6 e i ）                              (3a )

  在0.5l点，其变形量为

 （f₂）_0.5l = －5 q l⁴  / （ 96 e i ）                        (3b)

     (3) 受弯矩m_b的悬臂梁（见图6）

其变形曲线方程为

f₃ =  m_b x²/ （2 e i ）                                                  (4 )

 在b点，其变形量为

（f₃）_b =m_b l²/  2 e i                                                   (4a )

   在0.5l点，其变形量为

      （f₃）_0.5l =  m_b l²  / （ 8 e i）                                             (4b )

根据式（1a）和已知边界条件x=l, (f )_b=0，可以求出m_b，则

  m_a = m_b =    q l²/12                                                  (5 )

 又根据式（1b）求出在x=0.5l时，图3中的最大变形量为

     f_max =    q l⁴/ 384ei                                                              (6 )

 将分布载荷q = p₁ / l =（p sinφ）/ l = （ω²  rρbδl sinφ）/ l = ω²  rρbδsinφ和微元的惯性矩i = δ³ b / 12 ,以及弹性模量e = 2.06×10¹¹(pa)和钢的密度ρ = 7.85×10³(kg/m³), ω= 2πn / 60 (1/rad)代入式（6），则得出在叶片上任